Se puede afirmar con certeza que la mayoría de las personas que usan la estadística están más familiarizadas con los análisis paramétricos que con los no paramétricos. Las pruebas no paramétricas también se conocen como pruebas independientes de la distribución, porque no parten del supuesto de que los datos siguen una distribución específica.
Tal vez haya escuchado que se deben usar pruebas no paramétricas cuando los datos no satisfacen los supuestos de la prueba paramétrica, especialmente el supuesto acerca de la distribución normal de los datos. Eso suena como una elección clara y sencilla, pero hay otras consideraciones.
En esta publicación, le ayudaré a determinar cuándo debería usar un:
- Análisis paramétrico para probar las medias de los grupos.
- Análisis no paramétricos para probar las medianas de los grupos.
En particular, me centraré en una razón importante para usar las pruebas no paramétricas que creo que no se menciona con suficiente frecuencia.
Pruebas de Hipótesis de la Media y la Mediana
Las pruebas no paramétricas son como un universo paralelo a las pruebas paramétricas. La tabla muestra pares relacionados de pruebas de hipótesis que se ofrecen en Minitab Statistical Software.
Pruebas paramétricas (medias) | Pruebas no paramétricas (medianas) |
Prueba t de 1 muestra | Signos para 1 muestra, Wilcoxon para 1 muestra |
Prueba t de 2 muestras | Prueba de Mann-Whitney |
ANOVA de un solo factor | Kruskal-Wallis, Prueba de la mediana de Mood |
DOE factorial con un factor y una variable de bloque | Prueba de Friedman |
Razones para Usar las Pruebas Paramétricas
Razón 1: Las pruebas paramétricas pueden funcionar bien con distribuciones asimétricas y no normales
Esto puede ser una sorpresa, pero las pruebas paramétricas pueden funcionar bien con datos continuos que no son normales si se cumplen las pautas relativas al tamaño de la muestra que se indican en la siguiente tabla. Estas pautas se basan en estudios de simulación realizados por expertos en estadística aquí en Minitab. Para saber más sobre estos estudios, lea nuestros Artículos técnicos.
Análisis paramétricos | Pautas sobre el tamaño de la muestra para datos no normales |
Prueba t de 1 muestra | Mayor que 20 |
Prueba t de 2 muestras | Cada grupo debería ser mayor que 15 |
ANOVA de un solo factor |
|
Razón 2: Las pruebas paramétricas pueden funcionar bien cuando la dispersión de cada grupo es diferente
Aunque las pruebas no paramétricas no presuponen que los datos siguen una distribución normal, sí tienen otros supuestos que pueden ser difíciles de cumplir. Para las pruebas no paramétricas que comparan grupos, un supuesto común es que los datos de todos los grupos tienen la misma dispersión. Si los grupos tienen una dispersión diferente, las pruebas no paramétricas podrían no proporcionar resultados válidos.
Por otro lado, si utiliza la prueba t de 2 muestras o el ANOVA de un solo factor, simplemente puede ir al cuadro de diálogo secundario Opciones y desmarcar Asumir varianzas iguales. Voilà, ¡puede continuar aunque los grupos tengan dispersiones diferentes!
Razón 3: Potencia estadística
Las pruebas paramétricas suelen tener más potencia estadística que las pruebas no paramétricas. Por lo tanto, es más probable detectar un efecto significativo cuando realmente existe uno.
Razones para usar las Pruebas no Paramétricas
Razón 1: Su área de estudio se representa mejor con la mediana
Este es mi motivo favorito para usar una prueba no paramétrica, ¡y uno que no se menciona con suficiente frecuencia! El hecho que se pueda realizar una prueba paramétrica con datos no normales no implica que la media sea la mejor medida de la tendencia central para los datos.
Por ejemplo, el centro de una distribución asimétrica, como los ingresos, puede medirse mejor con la mediana, donde el 50% está por encima de la mediana y el 50% está por debajo. Si usted agrega varios multimillonarios a una muestra, la media matemática aumenta enormemente aunque el ingreso de la persona típica no cambia.
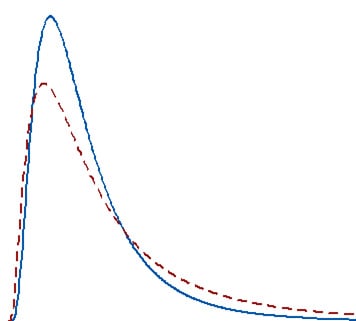
Cuando la distribución es lo suficientemente asimétrica, la media se ve afectada fuertemente por cambios que ocurren lejos, en la cola de la distribución, mientras que la mediana sigue reflejando con mayor precisión el centro de la distribución. Para estas dos distribuciones, una muestra aleatoria de 100 proveniente de cada distribución produce medias que son significativamente diferentes, pero medianas que no son significativamente diferentes.
Otras dos publicaciones de blog ilustran bien este punto:
- Uso de la media en el análisis de datos: No siempre es una decisión acertada
- La economía no paramétrica: ¿Qué significa promedio en realidad?
Razón 2: El tamaño de la muestra es muy pequeño
Si no cumple con las pautas relativas al tamaño de la muestra para las pruebas paramétricas y no está seguro de tener datos distribuidos normalmente, debe usar una prueba no paramétrica. Cuando usted tiene una muestra realmente muy pequeña, incluso es posible que no pueda determinar la distribución de los datos, porque las pruebas de distribución carecerán de la potencia suficiente para proporcionar resultados significativos.
En este escenario, usted se encuentra en un punto difícil sin ninguna alternativa válida. Para comenzar, las pruebas no paramétricas tienen menos potencia, y el golpe es doble si a eso se agrega un tamaño de muestra pequeño.
Razón 3: Usted tiene datos ordinales, o valores atípicos que no puede eliminar
Las pruebas paramétricas típicas solo pueden evaluar datos continuos y los resultados pueden verse afectados significativamente por los valores atípicos. Por el contrario, algunas pruebas no paramétricas pueden ser usadas con datos ordinales y no verse seriamente afectadas por los valores atípicos. Asegúrese de comprobar los supuestos para las pruebas no paramétricas, porque cada una tiene sus propios requisitos de datos.
Si tiene datos con una escala Likert y desea comparar dos grupos, lea mi publicación La mejor manera de analizar datos Likert: Prueba T de dos muestras vs. Mann-Whitney.
Reflexiones Finales
Comúnmente se piensa que la necesidad de elegir entre una prueba paramétrica y no paramétrica surge cuando los datos no cumplen con un supuesto de la prueba paramétrica. Tal puede ser el caso cuando se tiene un tamaño de muestra pequeño y datos no normales. Sin embargo, hay otras consideraciones importantes, porque frecuentemente las pruebas paramétricas pueden ser usadas con datos no normales. Por el contrario, las pruebas no paramétricas tienen supuestos estrictos que no se pueden pasar por alto.
La decisión depende de si la media o la mediana representa con mayor precisión el centro de la distribución de los datos.
- Si la media representa con exactitud el centro de la distribución y el tamaño de la muestra es lo suficientemente grande, considere una prueba paramétrica, ya que tienen mayor potencia.
- Si la mediana representa mejor el centro de la distribución, considere la prueba no paramétrica incluso si tiene una muestra grande.
Por último, si tiene un tamaño de muestra muy pequeño, puede que no tenga más opción que usar una prueba no paramétrica. ¡Por favor, recoja más datos la próxima vez si tiene la posibilidad de hacerlo! Como puede ver, las pautas en cuanto al tamaño de la muestra no son tan grandes en realidad. La probabilidad de detectar un efecto significativo en caso de que exista puede ser muy pequeña si el tamaño de la muestra es pequeño y se tiene que usar una prueba no paramétrica menos eficiente.
Comentarios
Publicar un comentario