
Las estadística inferencial son técnicas explicativas que utilizan muestras representativas de una población para comprobar la certeza de nuestras afirmaciones (llamadas hipótesis).
Esta certeza se expresa en términos de probabilidad.
Si la probabilidad es alta, entonces consideraremos que la afirmación «es correcta» (o al menos que no podemos rechazarla). En caso contrario, si la probabilidad de que nuestra afirmación sea cierta es baja, la rechazaremos por incorrecta. Es lógico, ¿verdad?
El problema muchas veces viene en el momento en el que queremos seleccionar la prueba estadística correcta.
Obtén más información de nuestro Máster de Estadística con R (XI edición)
Pero para ponértelo fácil voy a resumírtelo en tan solo dos preguntas: ¿Cuál es tu objetivo? y ¿Qué tipo de datos tienes?.
Y… ¡al final de este post te resumo las funciones que debes usar en R para llevar a cabo cada análisis!
El camino a seguir
La siguiente figura indica a grosso modo el camino a seguir mediante un mapa de las técnicas usuales de asociación y comparación.
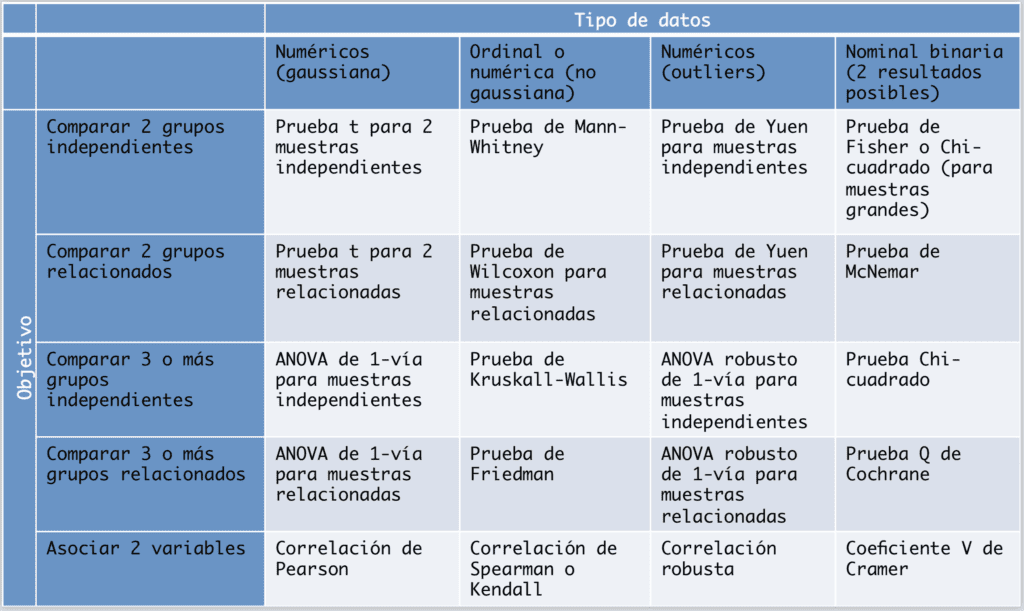
1. ¿Cuál es tu objetivo?
Asociar o comparar
Podemos distinguir entre dos objetivos principales para las técnicas explicativas: ASOCIAR O COMPARAR.
Ambos buscan establecer relaciones (semejanzas o diferencias) entre elementos pero, a diferencia de las pruebas de asociación, las pruebas de comparación evalúan estas relaciones entre uno o varios grupos.
Veamos un par de ejemplos para identificar el tipo de preguntas que intentan responder ambos tipos de técnicas:
- ASOCIACIÓN. ¿Existe algún tipo de relación significativa entre las variables?, ¿cómo es esta relación (positiva o negativa)?, ¿qué tan fuerte es la relación (magnitud)?, ¿la relación se mantiene si controlamos la influencia de terceras variables?.
- COMPARACIÓN. ¿Cuál es el promedio/variabilidad de la variable de estudio en la población?, dado un conjunto de poblaciones ¿son similares?, ¿entre cuáles de ellas hay diferencias significativas?, ¿qué variables explican esas diferencias? y ¿existe interacción entre las variables explicativas?.
Si quieres profundizar aún más en la selección de las técnicas explicativas debes considerar cómo son tus muestras (independientes o relacionadas).
¿Qué tipo de muestras tienes?
También debes saber distinguir cómo son tus muestras:
- Muestras independientes: cada observación corresponde a un sujeto o caso distinto.
- Muestras relacionadas (o pareadas): tenemos varias observaciones del mismo sujeto o caso. Las muestras relacionadas aparecen en experimentos del tipo antes-depués, como por ejemplo el estudio de pacientes donde se comparan los resultados antes y después de la aplicación de un tratamiento.
Ejemplo.
Imaginemos que queremos estudiar el efecto de un fármaco que presuntamente reduce la presión arterial. El problema puede estar planteado de dos maneras distintas según se consideren muestras relacionadas o independientes:
- Se toman 30 pacientes hipertensos al azar, se les suministra elfármaco a 15 de ellos y a los otros 15 se les aplica un placebo.Transcurrido un tiempo se miden las presiones sanguíneas deambos grupos y se contrasta si las medias son iguales o no.
- variable respuesta: presión sanguínea (numérica)
- variable explicativa: grupo (categórica: tratamiento y placebo). Las dos muestras están formadas por individuos distintos, sin relación entre sí: muestras independientes.
- Se administra el fármaco a los 30 pacientes hipertensosdisponibles y se anota su presión sanguínea antes y despuésde la administración del mismo.
- variable repuesta: presión sanguínea (numérica).
- variable explicativa: tiempo (categórica: antes y después de aplicar el fármaco). En este caso los datos vienen dados por parejas (presión antes y después) por lo cual los datos están relacionados entre sí: muestras relacionadas.
2. ¿Qué tipo de datos tienes?
¿Cómo son tus variables?
Seguro que tienes claro cuáles son los tipos de variables, así comienzan el 99% de los cursos de estadística de grado, pero hagamos un pequeño repaso para desempolvar estos conceptos.
Tenemos variables categóricas, que son de dos tipos: las llamadasvariables nominales (que son categorías sin orden) como el sexo; ylas variables ordinales (que sí representan un orden), como el nivelde estudios.
Recuerda que las variables nominales pueden ser binarias o dicotómicas (e.g. fumador/no fumador, enfermo/sano).
Por otra parte tenemos las variables numéricas, que pueden ser discretas si vienen dadas por números enteros, como el número de hijos, o continuas como el peso que se representa por números reales.
¿Se cumplen los supuestos clásicos?
En segundo lugar debes corroborar si tus datos cumplen o no con los supuestos de las pruebas estadísticas clásicas (normalidad, homogeneidad, independencia).
Esto te permitirá elegir entre pruebas PARAMÉTRICAS, pruebas NO PARAMÉTRICASy pruebas ROBUSTAS.
Para ello tienes que responder a las siguientes preguntas: ¿las variables se distribuyen según la curva normal (gaussiana)?, ¿los son grupos tienen dispersión similar (son homogéneos)?,
«All models are wrong, but some are useful «, Box (1979).
Cuando trabajas con datos reales en la mayoría de las ocasiones no se cumplen los supuestos de la estadística clásica.
En estos casos las técnicas paramétricas no nos demasiado útiles; pero como mencionamos en la entrada anterior (ver AQUÍ) tenemos 3 posibles soluciones:
- la transformación de los datos, cuando los datos no siguen una distribución normal o queremos disminuir su variabilidad.
- utilizar las pruebas no paramétricas cuando los datos no siguen una distribución normal
- utilizar las pruebas robustas cuando tienes datos atípicos.
Razones para utilizar pruebas paramétricas
- Si la distribución se aparta poco de la normalidad, y las muestras no son muy pequeñas (n>30), pueden ser válidas teniendo ciertos cuidados.
- Si la falta de homogeneidad de varianza en cada grupo no es muy grande, existen maneras en la prueba t o en el ANOVA de incluir esta condición. Sin embargo las no paramétricas no permiten solucionar este inconveniente.
- Generalmente tienen mayor poder estadístico que laspruebas no paramétricas. Es decir, con ellas tenemos más probabilidad de detectar un efecto significativo cuando realmente existe.
Razones para utilizar pruebas no paramétricas
- Si puedes utilizar contrastes que solo necesiten establecer supuestos poco exigentes (como simetría o continuidad) o quieres analizar las propiedades nominales u ordinales de losdatos.
Ten en cuenta que muchas de estas pruebas utilizan la mediana en lugar de la media para sus cálculos.
Cuando la distribución de frecuencias de los datos es muy asimétrica, la media se ve muy afectada mientras que la mediana refleja mejor la centralidad de la distribución.
- Cuando tienes un tamaño muestral pequeño.
Cuando tenemos pocos datos las pruebas de normalidad pierden poder estadístico y no estamos seguros del tipo de distribución de losdatos. Sin embargo, para realizar pruebas no paramétricas el tamaño muestral tampoco debe ser muy pequeño.
- Cuando analizamos datos ordinales o de rango.
Las pruebas paramétricas sirven para analizar datos de escala y sus resultados se ven muy afectados por la presencia de outliers. Aunque a veces la interpretación de los rangos medios puede ser difícil.
Razones para utilizar pruebas robustas
- Son estables respecto a pequeñas desviaciones del modelo paramétrico asumido (normalidad y homocedasticidad).
A diferencia de los procedimientos no paramétricos, los procedimientos estadísticos robustos no tratan de comportarse necesariamente bien para una amplia clase de modelos, pero son de alguna manera óptimos en un entorno de cierta distribución de probabilidad, por ejemplo, normal.
- Solucionan los problemas de influencia de los outliers.
- Son más potentes que las pruebas paramétricas y no paramétricas cuando los datos no son normales y/o no son homocedásticos.
- Los métodos robustos modernos son diseñados para obtener un buen desempeño cuando los supuestos clásicos se cumplen y también cuando se incumplen. Por lo tanto, haypoco que perder y mucho que ganar a la hora de utilizar estastécnicas en lugar de las clásicas.
Comentarios
Publicar un comentario